Приложение 1. Анализ стационарного
демографического состояния
Рассмотрим демографическую характеристику — вероятность для новорождённого прожить не менее лет:
Эта зависимость для стационарного состояния имеет универсальный, определяющий характер потому, что зная только её, можно найти большинство других характеристик; это позволяет назвать зависимость функцией жизни.
Уточним понятие стационарного демографического состояния. Стационарным будем считать такое состояние, когда не только общая численность людей , но и введенная характеристика — функция жизни, остаются неизменными во времени.
Зависимость обладает следующими свойствами:
- При () : каждый ребёнок, родившийся живым, проживёт какое-то, хотя бы самое небольшое время. Случаи рождения мёртвых детей бывают, но мы можем их исключить из нашего рассмотрения, не относя их ни к событиям рождения (влияющим на коэффициент рождаемости ), ни к событиям смерти (влияющим на коэффициент смертности ). При этом вероятность будет стремиться к 1 при .
- Существует максимальная продолжительность жизни , при которой вероятность обращается в нуль: никто не может прожить больше лет — это биологический предел.
- При всех значениях от до функция для стационарного состояния монотонно убывает (точнее, ни на одном участке не возрастает) от значения при до при . Монотонное убывание объясняется очень просто: для того, чтобы дожить, например, до 61 года, надо сперва дожить до 60 лет, причём вероятность дожить до 61 года меньше, чем до 60 лет, ибо существует некоторая вероятность смерти между 60 и 61 годами. В остальном зависимость может быть самой различной.
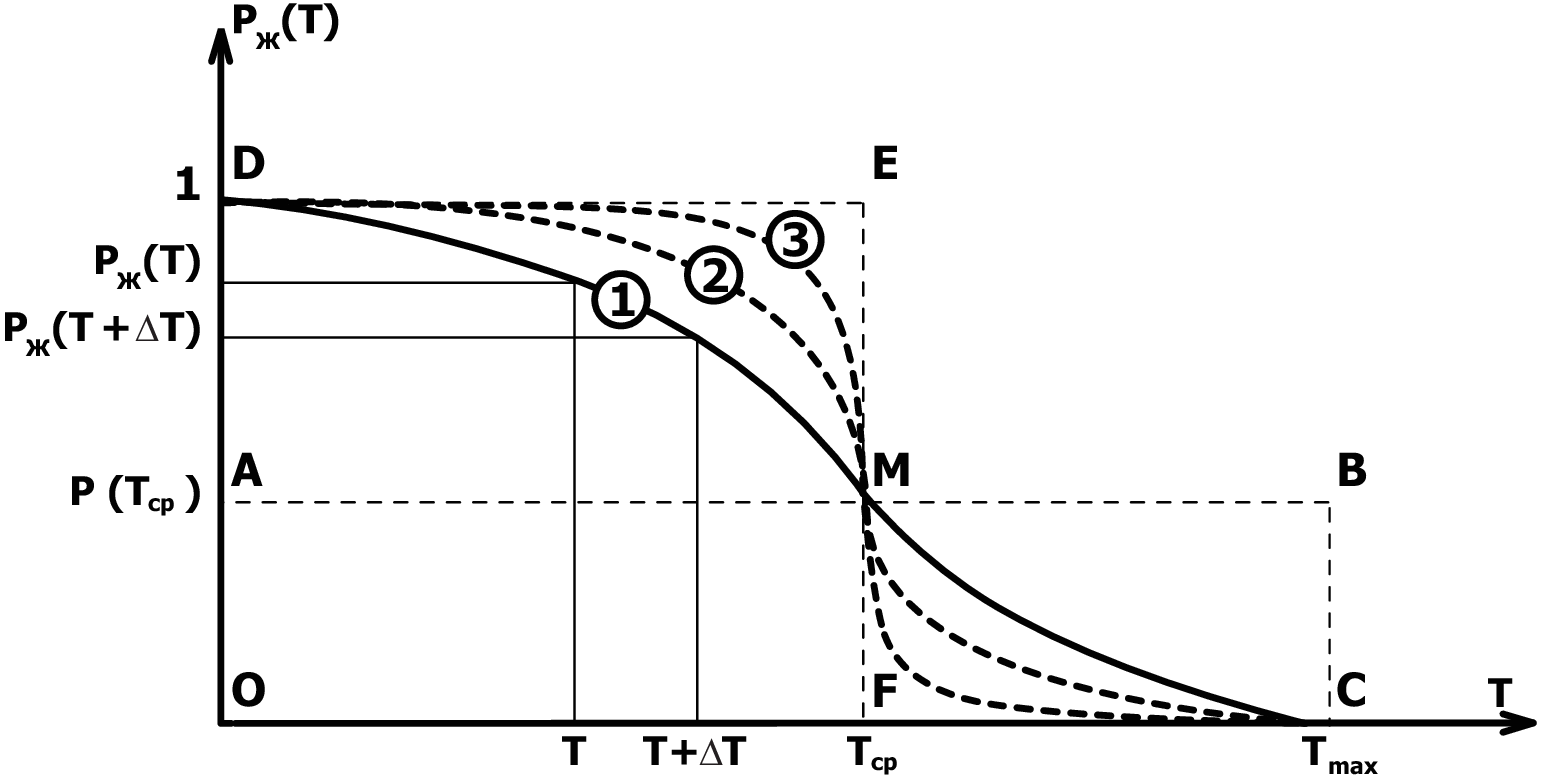
На рис. П.2 изображены четыре типа таких зависимостей:
-
-
1 — вероятность уменьшается равномерно; в этом случае смерть может наступить в любом возрасте от T = 0 до примерно с равной вероятностью;
-
-
2 — кривая, характеризующаяся повышенной смертностью в раннем (возможно, детском) возрасте;
-
-
3 — кривая, когда существует некоторая наиболее вероятная продолжительность жизни . В этом случае вероятность смерти в раннем возрасте мала и существует некоторая, сравнительно небольшая, вероятность дожить почти до максимального возраста . Наконец,
-
-
4 — кривая, при которой продолжительность жизни растёт и приближается к .
Располагая зависимостью , можно найти следующие характеристики:
- коэффициент рождаемости ; в стационарном состоянии он равен коэффициенту смертности: . При этом коэффициент естественного прироста равен нулю: ;
- относительную плотность и гистограммы, характеризующие распределение населения по возрасту;
- условную вероятность оставшейся продолжительности жизни, при условии, что человек уже прожил лет: ;
- плотность распределения продолжительности жизни и среднюю продолжительность ;
- оценить степень стабильности продолжительности жизни, т. е. разброс фактической продолжительности жизни относительно её среднего значения.
Рассмотрим связь этих характеристик с функцией .
1. Коэффициент рождаемости. Этот коэффициент был определён формулами (1.1) и (1.2) основного текста:
где — общее число людей в рассматриваемой группе; и — количество родившихся в этой группе за время и . Отсюда:
Из (или ) новорождённых до возраста доживает только часть, равная (или ). В любой момент времени именно столько людей из числа находятся в возрасте от до . Поэтому общее число людей в группе равно интегралу:
| (П1.3) |
Сокращая это выражение на , получим:
| (П1.4) |
Таким образом, коэффициент рождаемости однозначно определяется функцией .
2. Относительная плотность распределения людей по возрасту. Гистограммы. Вопрос типа «сколько людей (из группы в человек) находятся в возрасте 60 лет?», если его понимать буквально (т. е. точно 60 лет), не имеет смысла. Задавая такой вопрос, на самом деле имеют в виду «сколько людей находятся в возрасте от 60 до 61 года?» (ровно 61 год исключается; он не входит в этот диапазон). Говоря о количестве людей определённого возраста, всегда имеют в виду некоторый возрастной диапазон.
Когда всё же подобные характеристики необходимо обрабатывать математически, то вводят понятие о плотности распределения количественной характеристики по непрерывной шкале.
Под плотностью распределения группы из людей по возрасту понимается функция времени (возраста) , которая равна пределу
| (П1.5) |
где — временной интервал; — число людей, возраст которых находится в диапазоне от до .
Но поскольку группы и число людей в них могут быть разными, то удобнее, разделив на , рассматривать относительную плотность распределения людей по возрасту . Она равна:
| (П1.6) |
При получим начальное значение :
| (П1.7) |
Учтём теперь, что при есть число рождений за время , а равно числу людей из , доживших до возраста :
| (П1.8) |
Используя для формулу (П1.1) и подставляя это значение в (П1.6) и (П1.7), получим:
Таким образом, относительная плотность распределения людей по возрасту с точностью до постоянного множителя () равна функции жизни . В сущности — это одна и та же функция.
Пользуясь выведенными соотношениями для стационарного состояния, можно определять относительное число людей в любом возрастном диапазоне. Например, для диапазона получим:
| (П1.11) |
Это позволяет строить гистограммы, которые широко применяются в демографических расчётах и литературе. Они отражают относительное количество человек, т. е. процентный состав населения, определённых возрастных групп, например, от 0 до 14, от 15 до 60 и старше 60 лет ([5 и др.]), или с интервалами через 5 лет и т. д. На рис. П.3 показан пример такой гистограммы с интервалами лет. Из рисунка видно, что в возрасте от 0 до 10 лет находится 22% всего населения, в возрасте от 10 до 20 лет — 19% и т. д. Видно, что численность людей монотонно уменьшается с возрастом, сначала медленно и равномерно до 50 лет, затем быстрее в возрасте 50–60 лет. Число людей старше 70 лет относительно невелико.
Для перехода к абсолютным величинам любую относительную характеристику достаточно умножить на — число людей в рассматриваемой группе.
3. Условная вероятность оставшейся продолжительности жизни. Эта характеристика определяет вероятность для человека, прожившего лет, дожить до возраста . Данная зависимость может быть получена из кривой следующим образом. Разделим все ординаты кривой для значений на ординату . При этом получится кривая, имеющая смысл для и равная 1 при . Её значения для различных и определяют искомую условную вероятность. На рис. П.4 показана эта процедура.

- Исходная зависимость .
- Условная вероятность прожить не менее лет, при условии, что человек прожил лет — .
4. Плотность распределения продолжительности жизни и средняя продолжительность . Продолжительность жизни относится к тем характеристикам, которые должны описываться с помощью плотности вероятности.
Рассмотрим два момента времени и (см. рис. П4). Вероятность дожить до этих моментов равна соответственно и . Следовательно, вероятность смерти в интервале от до равна:
| (П1.12) |
Разделив это выражение на , и переходя к пределу при , получим с одной стороны значение плотности вероятности смерти в возрасте — , а с другой стороны производную от функции со знаком минус:
| (П1.13) |
Средняя продолжительность жизни равна интегралу:
| (П1.14) |
Используем теперь формулу интегрирования по частям:
где ; ; .
При этом:
Первое слагаемое в этом выражении обращается в нуль, т. к. при первый, а при второй сомножитель равен нулю. Поэтому окончательно получим для средней продолжительности жизни:
| (П1.15) |
где — площадь, ограниченная функцией .
На рис П.5 изображен прямоугольник ОАВС, равный по площади , и, следовательно, , и также равный по площади прямоугольник ОDЕF с ординатой, равной 1, и абсциссой : . Общая точка M пересечения сторон AB и EF этих прямоугольников лежит на кривой 8 и может быть названа точкой средней жизни.
5. Стабильность продолжительности жизни. Иногда может представлять интерес вопрос о стабильности продолжительности жизни, т. е. о разбросе реальной продолжительности жизни конкретных людей по отношению к . Подобные характеристики чаще всего оцениваются через дисперсию или среднеквадратичное значение разностей между фактическими величинами (в данном случае фактическими возрастами смерти) и средним значением. Однако возможны и другие способы оценки стабильности. В частности, стабильность продолжительности жизни людей может быть оценена величиной площади криволинейных треугольников DEM и MFC (рис. П.5). Из рисунка легко увидеть, что эти две фигуры по площади равны: , поскольку . Поэтому для оценки стабильности можно использовать одну из этих площадей:
| (П1.16) |
На рис. П.5 пунктиром изображены ещё две кривые жизни — 2 и 3, отличающиеся большей, чем кривая 1, стабильностью при одной и той же средней продолжительности жизни . Кривые 2 и 3 всё ближе примыкают к ломаной линии DEFC. По-видимому, человечество заинтересовано в увеличении стабильности продолжительности жизни и приближении к биологическому пределу .
Безусловно, наряду с относительными представляют интерес абсолютные характеристики: распределение населения по возрасту, рождаемость, общая численность и др. Для решения этих вопросов с помощью зависимости достаточно знать какую-либо одну из абсолютных характеристик, например, общее число людей или число людей какой-либо одной возрастной группы и т. д.
Так, абсолютная численность населения в возрасте от до равна относительной численности (формула П1.11), умноженной на :
| (П1.17) |
Отсюда, зная и располагая зависимостью , можно найти для любых значений и или построить гистограмму типа рис. П.3 для любых интервалов . Можно, наоборот, по значению для какой-то одной возрастной группы найти и значения для любых остальных возрастных групп .
Аналогичным способом могут быть найдены и другие абсолютные характеристики.
В связи со сказанным выше следует отметить два момента:
- Построение зависимости для стационарного или близкого к нему демографического состояния по экспериментальным данным не обязательно требует изучения статистики на длительном временном интервале. Достаточно располагать данными о возрасте умерших в течение сравнительно небольшого промежутка времени (например, 1 года). По этим данным может быть построена зависимость — вероятность дожить до возраста .
- Рассмотренные выше соотношения могут оказаться полезными и для обычных демографических расчётов, когда демографический процесс не стационарен и происходит рост или уменьшение общей численности населения вследствие того, что рождаемость не равна смертности или когда изменяется характер кривой (например, вследствие уменьшения детской смертности или увеличения величины и т. д.).
В литературе иногда высказывается мнение, что увеличение численности людей в историческом плане происходит по экспоненциальному закону. По отношению к небольшим промежуткам времени это может приближенно выражать реальные процессы. Но в целом для значительных промежутков времени такое утверждение ошибочно.
В основе мнения об экспоненциальном росте в сущности лежат два момента:
- Теоретические расчёты показывают, что при неизменных значениях коэффициентов рождаемости и смертности изменение численности людей должно происходить по экспоненциальному закону (см. формулу (1.3) основного текста 1-й главы).
- Статистические данные о численности людей как будто бы (на первый взгляд и в отдельных случаях) это подтверждают.
Однако можно выдвинуть ряд возражений против такой точки зрения. Они состоят в следующем.
- Коэффициенты и всё время меняются под воздействием войн и эпидемий, изменений в условиях жизни людей, успехов по борьбе со смертностью, освоением новых источников питания, изменениями в экологической обстановке, в социальной сфере и многих других факторов.
- Простые расчёты, отражённые в табл. 1.4, показывают, что длительное существование человечества при неизменных и неравных между собой коэффициентах и невозможно.
- Существуют биологические пределы для коэффициента рождаемости и продолжительности жизни . А поскольку все люди смертны, то даже если бы все рождающиеся доживали до предельного возраста , всё равно очень быстро установилось бы равенство между числом рождений и смертей. Вопрос заключается только в том, при какой общей численности людей установилось бы это равенство.
- Всякая «гладкая» нелинейная функция на малом участке может быть приближённо представлена в виде экспоненты. Это может создать иллюзию экспоненциального роста, если рассматривать данные на небольшом отрезке времени.
- В литературе встречается такая характеристика, как период удвоения — время, в течение которого численность людей возрастает в два раза. Из статистических данных (см. табл. 1.2) видно и отмечается в литературе [7 и др.], что период удвоения всё время и значительно сокращается. Это ни в коем случае не характерно для экспоненты: при экспоненциальном росте период удвоения должен оставаться неизменным. Сокращение периода удвоения говорит о том, что рост населения происходит быстрее, чем по любому экспоненциальному закону.
- Это же подтверждается и анализом данных табл. 1.2. Например, логарифм экспоненциальной зависимости должен представлять собой линейную функцию. Однако анализ табл. 1.2 это не подтверждает.
На рис. 1.3 (основной текст, гл. 1) показан общий рост населения. Видно, что в период с 400 г. до н. э. по 1600 г. рост не был монотонным; наблюдаются периоды спада, например, в 400 и 1400 годах. Быстрый рост, начавшийся с этого времени, привёл к тому, что численность людей достигла 1 миллиарда в 1800 году, 1,5 млрд. в 1900 г., несколько превысила 5 млрд. в 1990 и, по прогнозам ООН, обещает перевалить за 6 млрд. в 2000 году.
На рис. П.6 представлен рост населения Земли в целом и по основным регионам за тот же период в логарифмическом масштабе. По оси абсцисс отложена функция . Из этих графиков можно увидеть следующее.
- Наблюдаются колебания численности во всех регионах, хотя из- за логарифмического масштаба они выглядят сглаженными. Так, например, уменьшению функции в Америке с 1400 по 1600 годы от значения 1,59 до 1,08 соответствует трёхкратное уменьшение населения с 39 до 13 миллионов человек.
- Наблюдается падение численности в Азии с 0-го по 400 и с 800 по 1200 годы, в Европе с 400 по 800 годы, на территории России (СССР) с 1200 по 1400 годы, в Америке с 1400 по 1600 годы, в Австралии и Океании с 1750 по 1850 годы. Как показывает исторический анализ, это было вызвано нашествиями иноземных завоевателей, войнами, колонизацией, эпидемиями, голодом.
- Примерно с 1700–1800 годов во всех регионах начался бурный рост населения; в развивающихся странах он продолжается и поныне.
- Общий рост населения планеты с 1700–1800 годов происходит быстрее, чем по экспоненциальному закону. Это видно хотя бы из того, что кривая 1 на рис. П.6 не является линейной, а всё более круто устремляется вверх. Дополнительная иллюстрация к этому представлена на рис. П.7. Здесь построена экспонента 1, примерно отражающая рост населения в 1700–1800 годах — на отрезке времени, где логарифмическая кривая 1 на рис. П.6 имеет приблизительно линейный участок. Эта экспонента достаточно хорошо выражает (аппроксимирует) численность в 1700, 1750, 1800, 1850 годах. Но начиная с 1850 года население растёт всё быстрее и быстрее и кривая 2, отражающая реальную численность, всё более уклоняется вверх от экспоненты.
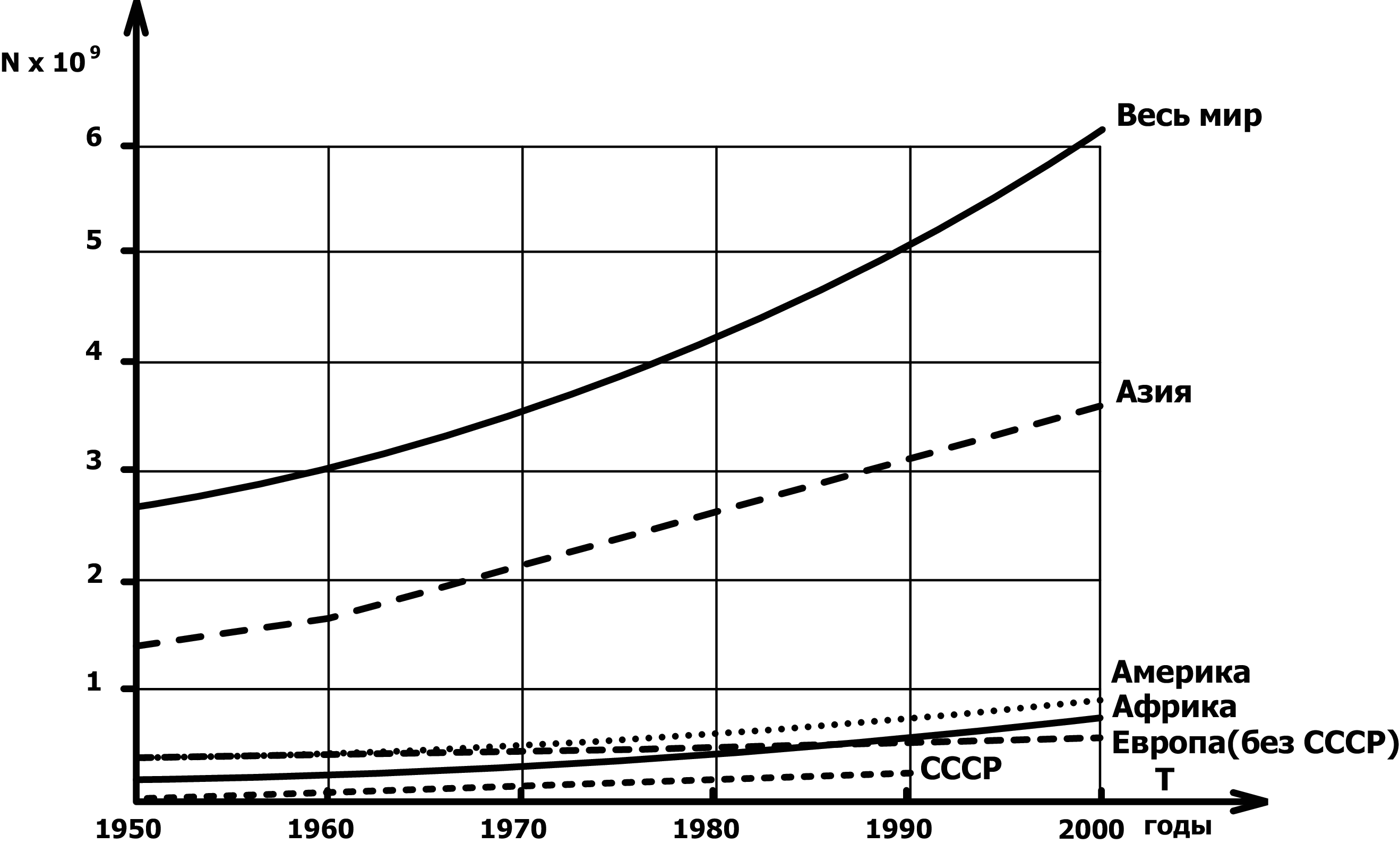
На рис. П.8 , построенном по данным табл. 1.3 и [5], показан рост населения на всей планете во второй половине 20 века. На этом рисунке по оси абсцисс отложена численность в миллиардах человек с шагом в 10 лет.
Всего за 40 лет с 1950 по 1990 годы население планеты возросло в 2,1 раза; в том числе в Азии (без СССР) — в 2,2 раза, в Африке — в 2,9 раза, в Америке — в 2,2 раза, в Европе (без СССР) — в 1,27 раза, в СССР — в 1,6 раза. В Австралии и Океании, которые на рис. 1.2 не отражены, также наблюдалось 2-кратное увеличение.9
Вместе с тем даже на этом графике видно снижение темпов роста в Европе и СССР. Это явление характерно для развитых стран; наблюдается оно также в США и Канаде (если их рассматривать отдельно), хотя и не в такой степени, как в Европе.

-
-
Функция .
-
-
Число людей N выражено в миллионах.

- Экспонента, аппроксимирующая рост населения в 1700 — 1800 годах.
- Фактический рост населения.
- Экспонента, аппроксимирующая рост населения в 1700 — 1800 годах.
- Фактический рост населения.