Приложение 2. Методика расчёта срока
исчерпания ресурсов
Пусть полный (в литературе употребляется термин потенциальный) мировой запас некоторого ресурса равен единиц (тысяч, миллионов или миллиардов тонн, баррелей или карат и т. п.), а его потребление (добыча) в настоящее время, которое мы примем за начало отсчёта (), равно единиц в год. Эту добычу можно представить как произведение числа жителей Земли на условное среднее потребление на одного человека в год :
| (П2.1) |
Предположим, что население Земли и среднее потребление на человека меняются по экспоненциальному закону:
| (П2.2) |
где и представляют собой относительный прирост (или убыль) населения и годового потребления на одного человека в единицу времени, т. е. за год:
Такое предположение в настоящее время и вообще для небольших промежутков времени близко к реальной действительности. Отметим, что эти формулы применимы к росту населения или потребления, когда или , стабильному состоянию при , , когда и равны нулю и случаю спада, когда или . Общее потребление также будет меняться по экспоненте:
| (П2.3) |
с общим показателем , характеризующим относительное изменение общего потребления в единицу времени:
| (П2.4) |
Итак, мы имеем запас , а расходовать его собираемся со скоростью
Этот запас будет исчерпан за время , которое определяется уравнением
| (П2.5) |
Отсюда находим :
Это и есть то время, в течение которого будет полностью истрачен весь запас. Надо только учитывать, что величина может быть положительной (рост потребления), нулевой (стабильное потребление) или отрицательной (спад потребления). Отрицательное значение может стать таким, что выражение, стоящее под знаком логарифма, будет равно нулю или отрицательным. В этом случае операция логарифмирования, которой мы воспользовались, становится незаконной и уравнения (П2.6), (П2.7) не имеют решения. Это означает, что спад добычи происходит слишком быстро и имеющийся ресурс никогда не будет исчерпан. При (стабильное потребление) правая часть выражения (П2.8) становится неопределённой. Раскрывая эту неопределённость, получим тривиальное решение:
В формуле (П2.8) время в сущности зависит не от трёх параметров (, , ), а только от двух: и отношения :
Это выражение можно ещё более упростить, положив , и тогда
| (П2.9) |
Эта удобная формула позволяет определять сроки исчерпания любых ресурсов. Она показывает, что время заметно зависит от величины (темпов роста или спада потребления) и гораздо слабее зависит от , т. е. от текущего запаса , который известен очень ориентировочно, и от абсолютной величины добычи, которая известна хорошо.
Для пояснения сказанного рассмотрим конкретный пример. Возьмём каменный уголь — один из энергетических материалов. Его потенциальные ресурсы в развитых капиталистических и развивающихся странах согласно [21] оцениваются величиной миллиардов тонн (3,74 т), а добыча составляет 19 миллиардов тонн (2,19 т). Годовой прирост добычи за предшествующие 5 лет немного колебался, но в среднем (2,6% за год). Отсюда:
Предположим теперь, что при оценке мы ошиблись и приуменьшили запас в 10, в 100, … в 1000 раз.10 В этом случае 0; 5 лет; ; года; ; 6 лет. Конечно, для поколений, которые будут жить в ближайшие столетия, всё это важно, но для судеб человечества в течение миллионов лет это не имеет никакого значения.
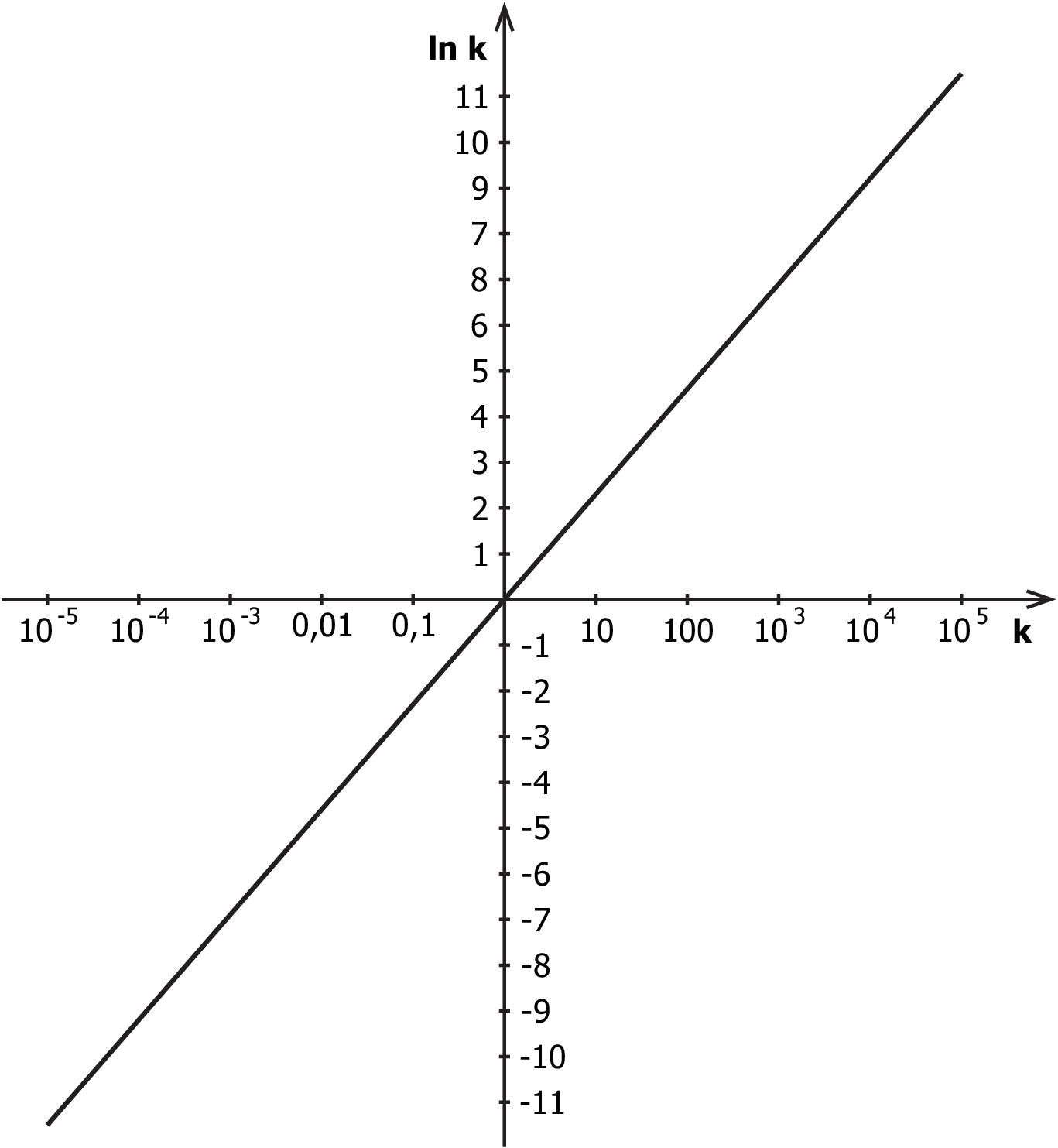
Рассмотрим теперь влияние темпов прироста добычи. Пусть при оценке мы ошиблись всего на 1,3%, т. е. в два раза: 013 (вместо 026). Тогда при т, и года, т. е. 1% ошибки в величине эквивалентен 10-кратной ошибке в . При стабилизации потребления угля, когда , наличных ресурсов хватит уже на 1700 лет, а если за счёт сокращения рождаемости при современном потреблении на одного человека (0,44 т/год) население начнёт уменьшаться всего на 1% в год (01),11 то ресурсы угля никогда не будут исчерпаны. Правда, к таким оценкам надо относиться с крайней осторожностью, ибо существует опасность, что через пару тысяч лет последний оставшийся на Земле человек будет размышлять, что делать с запасами каменного угля, которые так и не удалось использовать. А если рассуждать несколько серьёзнее, нетрудно подсчитать, что при сокращении численности населения всего на 0,1% в год (001), через 1600 лет человечество уменьшится в 5 раз — с 5 до 1 миллиарда. При этом будет использовано всего только т угля. Стабилизировав после этого численность человечества и потребление, можно спокойно жить ещё 4500 лет. Правда, в рассматриваемых масштабах это всё ещё очень малые сроки, но они позволяют обеспечить достаточный запас времени для спокойного перехода к новым источникам ресурсов, технологиям и вообще к новому укладу жизни. Изложенной методикой определения сроков можно пользоваться для любых видов ресурсов и любых условий. Читатель может проделать это и сам, причём даже без калькулятора, пользуясь только графиком зависимости , представленном на рис. П.9, и производя дополнительно самые несложные операции типа умножения и деления.